Education from a Hegelian perspective

G.W.F Hegel is not the most well-known philosopher, however, he massively influenced the musings of Karl Marx and Friedrich Engels and their writings on Communism and Socialism. Although Marx ultimately rejected the Hegelian view of the world as idealistic, it actually influenced Marxist philosophy quite drastically. Although I too feel it to be rather idealistic, I think it has some merit in explaining the current state of education.

Hegel’s principle of view of history posited that it was a series of events that displayed a process of development and that in order to understand one part, you must first understand the whole. I believe this notion parallels quite aptly with the state of modern education. In order to understand how teachers teach effectively now, we must first understand what methods teachers used before us and why they were deemed to be ineffective, or how our methods have grown from them. Furthermore, you cannot understand an individual concept within teaching, whether it be Constructivism or spacing, without first understanding education as a whole. Constructivism and spacing both co-exist and spawn from other theories that contradict them (e.g. Behaviourism and Blocking). In order to understand the merit of spacing, I must also understand the pitfalls of block teaching.

Each concept exists under the umbrella of education within which it manifests itself.  It can therefore be assumed that education is always developing, because each concept draws and improves upon concepts that have preceded it. In that sense, education is dynamic and imperfect, but has the capability and potential of achieving perfection, or so Hegel would have argued (this is why Marx deemed Hegel to be a bit of an idealist).

Unlike other philosophers, Hegel rejected the notion that philosophers should comment on or predict the future. His ideas focused on the zeitgeist of the period. This too mirrors the current state of educational theory and dialogue. We often analyse and comment on the contemporary condition of education, and often look backwards to do so, but we rarely comment on the future. This links back to Hegel’s view about the dynamic system that is always progressing by utilising the views that preceded it. In this sense, it is impossible to comment on the future because we have not yet had enough experience of the concepts that dominate the present zeitgeist. Perhaps a current example would be the idea of retrieval practice. We are unsure of what will follow it, or how it will be improved upon, because its prominence is very current and is yet to be held up to intense critique. At the moment of writing this, retrieval practice has swept across education as the saviour of ‘remembering more’ and ‘changes to long-term memory’. But overreliance on this concept without first truly critiquing it will inevitably lead to retrieval practice that is, at least in some part, rather ineffective. For example, the emphasised focus on low-stake quizzes tends to focus only on substantive knowledge and largely ignoring disciplinary knowledge. You can see more on that in these two blogs – https://mrmorgsthoughts.wordpress.com/2020/01/03/how-can-we-assess-knowledge/ and http://www.thatboycanteach.co.uk/2019/12/beware-reverse-engineered-curriculum-or.html

The Hegelian perspective is characterised by the idea that ideas can develop and progress by looking backwards. From this, Hegel’s view of the ‘dialectic’ was born. This entails that we must carefully examine an idea by linking it to other ideas (previous or current), either because it can contradict or complement it. So Hegel’s view of history was not just that of a simple list of events, but that history is the view of how all these events link together. Education again parallels this. All educational theory links together, whether you choose to adhere or align most to Piaget, Vygotsky or Skinner (those are the only big names I can remember from my PGCE). Where I think the ‘dialectic’ relates to education most is in its origins. The term originated in ancient Greece, whereby a ‘dialogue’ was established upon opposing views and this led to the formulation of truths. Hegel believed that by having these opposing views or contradictions, only then could we progress (I think a lot of EduTwitter trolls could learn a thing or two from that statement).

The ‘dialectic’ entails three steps. Thesis, Antithesis and Synthesis – always in that order. Thesis is the original idea that starts off the dialogue; antithesis is the contradicting idea that builds on this dialogue by presenting an opposing point of view; and synthesis is the reconciliation of these first two steps into a new, established truth. Of course, the synthesis part can be ongoing and challenged itself, and that is why we continue to have multiple new theories that are born out of singular, past ones. The process is very cyclical because of this. This led Hegel to conclude that changes can be gradual, but that they can have a very sudden impact (see retrieval practice mentioned above). Ergo, the state of education changes slowly for the most part, but with very sudden transformations.

Hegel determined that the ‘dialectic’ was governed by certain laws. The most relatable one of these laws to education being that of ‘the law of the unity of opposites’. This states that all things in the world exist in opposition to something else (e.g. hot and cold, short and long) – so too does educational theory (e.g. Constructivism vs Behaviourism) and every teacher’s opinion on Twitter!

 

I hope this made sense to someone. It mostly feels like nonsensical ramblings when I read it back. This is simply my interpretation of how the Hegelian perspective applies to the modern state of education and in part to EduTwitter. Still, I’m glad the sociology part of my undergrad degree finally came in use for something.

NB: For a better understanding of my ramblings, read through Rupert Woodfin and Oscar Zarate’s Marxism: A Graphic Guide. This blog was written after reading that book.

How can we assess knowledge?

Before we can discuss how to assess knowledge, we must first define what knowledge is. With regards to teaching, I believe in a rather simplistic dichotomy of knowledge: substantive and disciplinary.

Substantive knowledge is the knowledge produced by any specific academic subject. It is therefore sometimes referred to as ‘content’ knowledge. It is the knowledge you learn from a topic or unit. In science, this might be what respiration is. In geography, it might be about the economic development of a region. In art, it might be the style of Impressionism. You get the idea. Substantive knowledge is the knowledge children gather as established fact. The concepts, the words, the dates and so on.

In contrast, disciplinary knowledge is the understanding of how that knowledge was formed, how it continues to be formed and a general understanding of how that subject manifests itself and operates. In science, this may be understanding how a scientific investigation is conducted. In geography, this could be an understanding of how geographical fieldwork is undertaken. In history, it could be how we gather information from historical sources. Disciplinary knowledge is understandably harder to teach and arguably less common in classroom assessments than it is in external assessments (e.g. GCSEs). I am proposing we address this imbalance.

We need to think about the validity and reliability of the assessments we use with regards to these two types of knowledge. If our assessment only tests substantive knowledge, then has the pupil learnt about how the discipline itself operates? Likewise, if the assessment only tests the disciplinary knowledge, can we truly know if the pupils have learnt the content of the topic and successfully added to their schema of pre-existing knowledge? Therefore, arguably, our assessments must provide opportunity to assess both types of knowledge together or assess them individually. I suggest the latter.

Previously, at my school, we (regrettably) used KWL grids to assess children’s progress through a topic. A KWL grid assesses what a child knows ( K ), what a child wants to know ( W ) and what they have learnt ( L ). I always found the W section to be particularly frustrating, as children will always write the most absurd questions here that you never get any time to address in depth, or you simply don’t know the answer to because your limited subject knowledge exists outside the realm of their wild imagination and its far-fetched questions. So then, what is the point in allowing children to ask these questions?

We believed these assessments showed progression in children’s learning simply because the third column had more writing than the first column, but this was no real indicator of children being successful in their learning long-term. Moreover, there are many problems with an assessment of this type. First, they seem to only test substantive knowledge, as they only ask children to recall what they know. Secondly, the opportunity for recall is rather lacking. Just asking children to write down everything they remember without any retrieval cues is unsurprisingly rather ineffective. For us, we needed to ensure our assessments were more effective in the foundation subjects.

An example of a blank KWL grid:

I will use my most recent history topic of the Great Fire of London to model the two separate assessments we came up with.

Testing substantive knowledge – vocabulary wordbank. Children are provided words from the topic and then asked to write down what they know about them. These act as retrieval cues, rather than simply asking children to write down everything they know about a topic with no prompts. If they can’t think of anything, they simply leave it blank so the teacher is aware of what needs to be revisited. Children write in as much or as little detail as they can. The teacher can then assess their understanding by looking at the level of detail in their answer and how well they have linked it to other words and concepts learnt.

Testing disciplinary knowledge – answering questions linked to the discipline itself. This would always be conducted subsequent to the assessment on substantive knowledge, because children would need to draw on that substantive knowledge to help them. This assessment would focus on unpicking the elements of the subject discipline we wanted them to grasp (e.g. for history, that could be how historical knowledge has accumulated over time, the reliability of sources or the correlation between cause and effect). Below is an example of this type of assessment. Next to each question in red, I have added the disciplinary knowledge each question sought to assess. Children would be given more space to write their answers for this assessment, as it would provide more scope for more detailed answers.

With the recent emphasis on retrieval practice in education forums, it would be easy to ignore disciplinary knowledge and focus solely on substantive knowledge. But, both types of knowledge are equally as important as one another. They are inextricably linked and inform one another. Together, they allow children to formulate a schema of knowledge that allows them to understand and interpret each subject, as well as the world around them.

Follow me on Twitter – @MorgsEd

Using ‘spacing’ to redesign our geography curriculum

With the introduction of the new OFSTED inspection framework in Sept 2019, my school quickly realised we were not up-to-scratch with certain subjects in our curriculum. When the new curriculum was introduced in 2014, we should have been changing and redesigning our curriculum then, but for whatever reason, we didn’t.

I was tasked with examining the current state of our geography curriculum and asked to try and improve it. It’s probably worth mentioning here that I am no geography expert and that I’m not even a geography subject lead (our actual lead is part-time so I was drafted in to help). I spent an entire day out of class to think about our three Is (intent, implementation and impact) as laid out in the OFSTED framework and how to redesign our curriculum to suit what we wanted.

Our old geography curriculum looked like this:

We deemed it to be insufficient. There had been no careful thought or planning into it other than to make sure there was haphazard and sporadic curriculum coverage. Our enacted curriculum (the one we were teaching) matched the formal curriculum (the one the government made) rather poorly and only in a rather reductionist and functionalist way. We hadn’t considered that the formal curriculum did not dictate when to teach, how much to teach or even which year group to teach each topic in. Therefore, instead of looking at rainforests in-depth and frequently, they were taught for just the length of a single half-term in just one year group (as seen above). There was no opportunity to draw upon that knowledge later on in their geography learning. This was true for many topics that deserved better, more regular coverage and this was the driving force behind redesigning our curriculum for the better.

Intent – What did we want children to learn and how would we make it rich, in-depth and meaningful? How would our curriculum demonstrate this richness and depth? We concurred that our intent should be that we want the children to understand the world in its vast variety of contexts (rich and poor, hot and cold, northern and southern etc). Our school context is a poor one, in which the vast majority of children do not receive much ‘life experience’. We therefore wanted a curriculum that could provide a wealth of cultural capital, by looking at as much of the world as possible. For example, in meeting the curriculum objective about understanding geographical similarities and differences of a small area of the United Kingdom, and of a small area in a contrasting non-European country, we decided to use Edinburgh as our focus from the UK, rather than London, as our children live there and are already familiar with it. We also wanted children to remember more and would place a greater focus on long-term learning than before. Our previous complacency of using a ready-made scheme had prevented this. We simply assumed that there was great coverage of the curriculum, a lot of drawing on prior knowledge and revisiting of content, when simply, there wasn’t. It was up to us to make sure this was planned out effectively.

Implementation – How were we going to ensure this long-term learning and variety of contexts was covered? The answer to that question was utilising the concept of ‘spacing’ in our curriculum design. For those unfamiliar with this term, ‘spacing’ entails teaching content in depth and then revisiting it at multiple points. Normally, teachers will do this across the teaching of a single unit. At the start of each lesson, they may use a low-stake, retrieval-based quiz that asks children about learning from previous lessons on the same topic. While this is effective, we wanted to negate the previous problem of only teaching something like rainforests for just one term, in just one year group. We therefore applied the concept of spacing to our entire curriculum.

In the younger years, children would start to create their schema of knowledge by looking at things that were familiar to them from the curriculum – e.g. where they are from, where they live and local habitats. We would then revisit these throughout the rest of their time at our school. In reception, children would start to look at the things mentioned above. This would then be consolidated in years 1 and 2, when it was revisited alongside the teaching of seasons, countries and continents and weather patterns.

Coupled with the idea of using spacing, our curriculum also operated on a ‘zooming-out’ model. Children would start by learning about where they live. Children would ‘zoom-out’ to learn about the local area, then another region in the UK, then the UK as a whole, then northern Europe, then North America and so on. The idea behind this was that each new topic provided children with a chance to draw on previously learnt knowledge. When looking at a region of the UK and the UK as a whole, how did they compare? When looking at Northern Europe and North America, were they similar by both being in the northern hemisphere? What was different about them? The other reason for doing this was that it allowed more scope for curriculum coverage. Instead of just learning about rainforests for one topic, children could look at them in every unit. Are there any rainforests in northern Europe? Why not? Is it because northern Europe does not fall on the equator? OK then, what must the climate be like in northern Europe then as it must differ to that of a rainforest?

I also found it useful to look at individual topics and lay out how each one could meet the different curriculum strands, but also to write the rationale behind teaching it in that specific year group at that specific time. This helped to make the spacing effect more readily apparent and maintained that each topic built on the already existing schema of knowledge the children have.

Our new, working progress curriculum therefore ended up looking a bit more like this:

Impact – It is still a working progress, but it is far better than what we were previously working from. It is too soon to witness any real impact as of yet, but presumably our children will leave with a much more rich, in-depth understanding of the world than they would have done in the past few years. We left it late and were slow to react, but it’s nice to know we are heading in the right direction.

 

The Literacy of Numeracy Part 2: Explicit Vocabulary Instruction

This is the 2nd part of my ‘literacy of numeracy’ blogpost series. The first analysed the language used in SATs tests and suggested tips you can use in the classroom to help prepare children for the tests based off of the analysis. You can find part 1 here – https://mrmorgsthoughts.wordpress.com/2019/02/24/ks2-maths-sats-language-analysis/ and a free downloadable version with a PowerPoint you can use in class here – https://www.tes.com/teaching-resource/ks2-maths-sats-language-analysis-12076440

 

I originally delivered this current blog as a 30-minute speech at an education conference and have tried my best to trim it down.

Introduction

In this blog series, I have been titling the posts under the umbrella phrase – ‘the literacy of numeracy’. I want to begin by clarifying what I mean by that. This phrase concerns itself with the disciplinary literacy of mathematics. Put more simply, ensuring each child is numerically literate by teaching them how to interpret visual symbols, graphs, charts, diagrams as well as individual terms and word problems. I believe language is the principle factor in developing this literacy within children and that the teaching of reasoning and problem solving in its current form can be very ineffective, when it relies on basic strategies like the use of RUCSAC and circling and underlining keywords.

Following a more language-specific method can prove to be more fruitful, as mathematics presents a lot of issues through its frequent variety of representation (e.g. 500g, 0.5kg and 1/2kg), but often the language used remains consistent. Maths can be considered as an additional language, in which it has its own specific terms and syntax. Enumerated below are just a few language obstacles children face in our classrooms:

1. Their knowledge of synonyms usually linked to one of the four calculation types (take instead of subtract, product instead of answer, altogether rather than add)
2. Their understanding of superlatives (biggest, largest, tallest, smallest)
3. Words that can have different meanings outside of a mathematical context (round, product, factor, prime)
4. Words other than superlatives that suggest comparison (between, more/less than, each, share, in order, sorting, put in the correct place)
5. Their understanding of the difference between the right answer and the wrong answer (best estimate, explain why Jack is not correct, write the correct symbol in each box, circle the improper fraction that is equivalent)
6. Verbs implying mathematical meaning (remaining, left, combine, collect, spend)

7. Compression of vocabulary through nominalisation and noun phrases – prime number, improper fraction, roman numeral, perpendicular and parallel lines, 3D shape
8. Abstract nouns – circumference, multiplication, area, perimeter

 

I emphasise this idea of maths as its own language, because as a maths SATs marker this year, I saw countless children incorrectly answer Reasoning Paper 2 Q18 (pictured below) because they indicated that ’95 goes into 5′ and ’87 goes into 3′. In my two years of SATs marking, I have seen far too many marks lost to inarticulation. Interestingly, in the 1068 responses to Paper 2 Q18 I marked, I only saw 1 child use the term ‘composite’. Naturally, you did not need to use this term to explain the answer correctly but I thought it was indicative of a wider issue: the lack of explicit vocabulary teaching in mathematics. Somebody once said that, “you shall know a word by the company it keeps”. While this may be true in fictional texts, these context clues aren’t always as evident in the world of maths. While normal vocabulary instruction often permits the use of analogy or synonym, the opposite is true in teaching the vocabulary of maths – where a singular definition is required and needs to be precise. Naturally, synonyms are still rife in maths (e.g. multiply, times), but the focus must be on teaching specific maths vocabulary, in order for children to be able to reason and problem solve freely without difficulty, especially as the style of language and vocabulary used in the non-fiction texts of the maths classroom are different in nature to the fiction texts children usually read.

 

Making it Accessible for All

As should be our intent for all our teaching, we must make the learning accessible for all in the classroom: our use of language is how we achieve this. Typically, the language that children read is more difficult than the language we use in our interactions with them. Therefore, there are two effects I believe to be present in the classroom. Firstly, the Dunning-Kruger effect, where children think they understand, but are unable to accurately communicate their thoughts and reasoning. Secondly, we as teachers suffer from the ‘curse of knowledge’, because we are experts transferring knowledge to novices, and we naturally overestimate their background knowledge and starting points. A consistent approach based around keywords is needed to combat both of these effects successfully. After all, the underlying fabric of maths teaching is to develop cognitive growth and the ability to reason, not to simply stack pieces of knowledge on top of each other.

 

Are the children that Alex Quigley defines as ‘word poor’ ever able to achieve mastery or greater depth? Language is an inevitable obstacle for them. This can be in part attributed to the fact that too much academic vocabulary remains implicit (e.g. explain, estimate, identify). These words require explicit vocabulary instruction, like any other word being learnt in any other subject. The language of the classroom and our everyday language are intertwined and should be more distinctly separate. For example, we may say that ‘we take from here and put it there’ rather than ‘we transfer from the hundreds column into the tens column’. We cannot successfully construct and convey the meaning of mathematics if we rely so heavily on language from everyday usage. The use of keywords is a simple way to combat this, as it allows for a manageable consistency; understanding can then be mapped and revisited more easily and it makes retrieval far simpler. As a year 6 teacher, I always thought about this approach when considering the transition to secondary school. The use of keywords in specific topics is likely to be consistent between our lessons in primary and secondary, whereas the use of individual and personal colloquialisms will not necessarily pervade.

 

Implementation

For me, this approach was born out of necessity. Working memory was becoming worse with each new class and the SATs were becoming increasingly hard following the introduction of the new curriculum – there seemed to be an increased demand on retrieval ability and the old level 6 questions were now arguably integrated at the back of the reasoning papers. I wanted to create an approach that was easy for teachers to remember and easy for them to implement. I ended up with two simple questions that we wanted the children to ask themselves:

• What does the question want us to find out? (i.e. how many litres left, a fraction of the shape etc)
• What do we have to do in order to find that answer? (i.e. subtract from the total, change to equivalent fractions etc)

The idea of these two questions is to blur the traditional gap between the words on the page (questions) and the words in our head (thought process) and we can achieve this through explicit vocabulary instruction. Research shows that children who are exposed to explicit vocabulary teaching benefit 3 times more than those who are not. In that sense, reasoning and problem solving activities must be treated as their own genre of reading that requires comprehensions skills taught around it (see part one of the blog for more on that). In order to do so, we must place an increased focus on both academic (e.g. estimate, identify) and subject-specific (e.g. numerator, multiple) vocabulary, like we do so readily in other subjects.

Children from Year 2 up can be taught to write down their reasoning justifications. Within these, they should be encouraged to use keywords to demonstrate their knowledge of them and how they exist within their own mathematical concepts. This should be done frequently, with at least one opportunity for it every lesson (e.g. a starter or plenary, responding to a further learning question from your marking).

In assessing children’s knowledge of keywords, Cronbach’s (1942) dimensions of word knowledge is a useful guide. It is also very informative as to how we should plan and deliver our lessons:

1. Generalisation – the ability to define a word
2. Application – the ability to apply the word in appropriate situations
3. Breadth – the ability to know and recall different meanings of the word
4. Precision – the ability to recognise exactly in what situations the word does and does not apply
5. Availability – the ability to use the word in our thinking and in our speech

Here is a basic example of a child in my class using the keywords they have been taught to confidently explain their reasoning (isosceles):

 

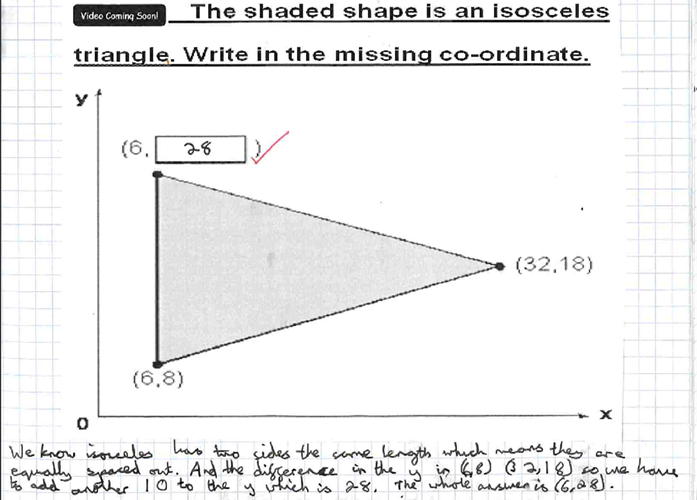
‘We know isosceles has two sides the same length which means they are equally spaced out. And the difference in the y is (6,8) (32, 18) so we have to add another 10 to the y which is 28. The whole answer is (6, 28).

Children need to be provided with the opportunity to reason frequently and our lessons can allow this through both verbal (answering questions aloud, discussions etc) and written opportunities (writing down their reasoning, independently attempting problems etc). The former being more important lower down the school (EYFS, Year 1), as younger children’s listening and speaking skills are superior to their written and reading skills. But no matter how good the opportunities we provide are, the only way this can be truly successful is for us to have the ability to improvise and respond effectively to whatever children say to us. That sounds easier said than done, and it is, but I believe as long as we have a depth of subject knowledge and are well aware of the common misconceptions children have, then we can improvise fairly effectively.

When it comes to introducing and teaching the definitions of words, I have found it effective to change definitions regularly so that children weren’t reliant on memorising a single definition and had to constantly access prior knowledge each time a new definition was formulated – for example, this could include blacking out words in a definition or providing different accompany examples to ones they have previously seen. But definitions aren’t enough. We need rich instruction. Here are just a few examples of things we can do to provide this alongside our definitions:

• use of pictorial representation
• etymology
• morphology
• root words (vertere = to turn)
• links to other words and concepts (vertex, inverse, convert and vertical – what is the link?)
• examples and non-examples
• keywords in lesson objectives (and discussing these LOs)
• frequent reasoning opportunities that use keywords and encourage children to use the keywords

Further comments about the use of keywords:

• We should employ a specific focus on visual representation alongside them, as often a child’s lack of vocabulary can hinder them in understanding new words being taught to them and it can make it hard for them to break down even the simplest of definitions. It is often these children that argue they ‘cannot do maths’ when simply they are unable to use mathematical language to explain their thoughts.
• Discussion of keywords is of the utmost importance because we must create an atmosphere where all answers want to be heard – right or wrong. We cannot develop understanding and take children to the next level without knowing if they misunderstand first.
• We must make the work accessible for the children who struggle more – do not give a year 6 child year 4 work. Give them year 6 work that is pitched at their level (more pictures, breakdown of keywords used, methods explicitly stated alongside keywords etc).
• If the meaning of keywords is only ever presented by the teacher and not negotiated with the class, then children will never consciously construct meaning for themselves. Meaning is derived from the context within which the language is being used, and the dialogue between teacher and child is what frames this.

 

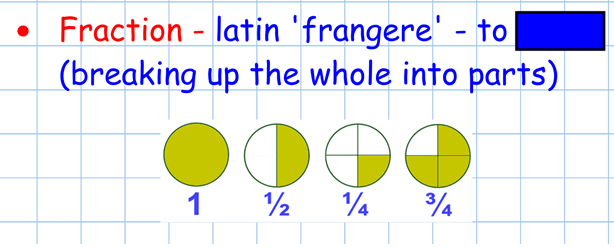
Here is a picture of a slide that I might typically show at the start of a lesson to my class. It includes a pictorial representation of the definition as an example, the root word and a part blacked out to challenge their thought on what the definition is:

 

I’ll end this blog with Charles Darwin’s very apt description of mathematics – “A mathematician is a blind man in a dark room looking for a black cat which isn’t there”. Language is the light that can help to cure the blindness, illuminate the room and put the black cat right in your hands.

I plan on carrying on this series by writing about mastery in maths and what a perfect lesson might look like, with reference to what has been said above.

Contact me on Twitter if you have any questions – @MorgsEd